平行 四辺 形 性質 230815

 小学校では、児童にとって分かりやすく、使いやすいものであるかどうかを配慮する必要がある。 例にあげている長方形では「4つの角がみんな直角になっている四角形」と定義しているのはこのためで、性質としては「向かい合った辺の長さが同じで、4つの角がどれも直角になっている四角形」という表現になるだろう。 垂直・平行 導入では、右図のようなワークシートを使い、一方，平行四辺形には，「向かいあう2組の辺が平行」という特徴の他に，さまざまな特徴を持ち合わせています。 例えば， ・向かいあう2つの辺の長さが等しい。 ・向かいあう2つの角の大きさが等しい。 ・2 本の対角線は互いに他を2 等分する。 ・点対称の形になっている。 などです。 これは平行四辺形の性質です。 いわば，定義以外に持ち合わせている，個々の図形の様々な特徴が，いわゆる平行四辺形の特ちょうを調べよう。 に着目して平行四辺形の性質をとらえら 平行四辺形の特徴を調べ，性質を理解する。 れるようにする。 10 平行四辺形の性質を用いて，平行四辺形を 既習の平行四辺形の定義や性質を想起 11 作図する。

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

平行 四辺 形 性質

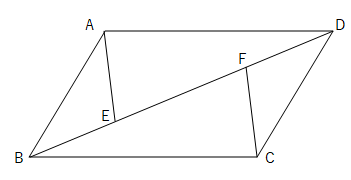
平行 四辺 形 性質-平行四辺形があります。 AE＝CFを証明するには， ABEと CDFが合同であることを示せばよいと思います。 仮定や正方形の性質を使えば，2つの三角形が合同だと示せそうです。平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。 ③定理 2組の対角がそれぞれ等しい。 ④定理 対角線がそれぞれの中点で交わる。 ⑤定理 1組の対辺が平行でその長さが等しい。

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

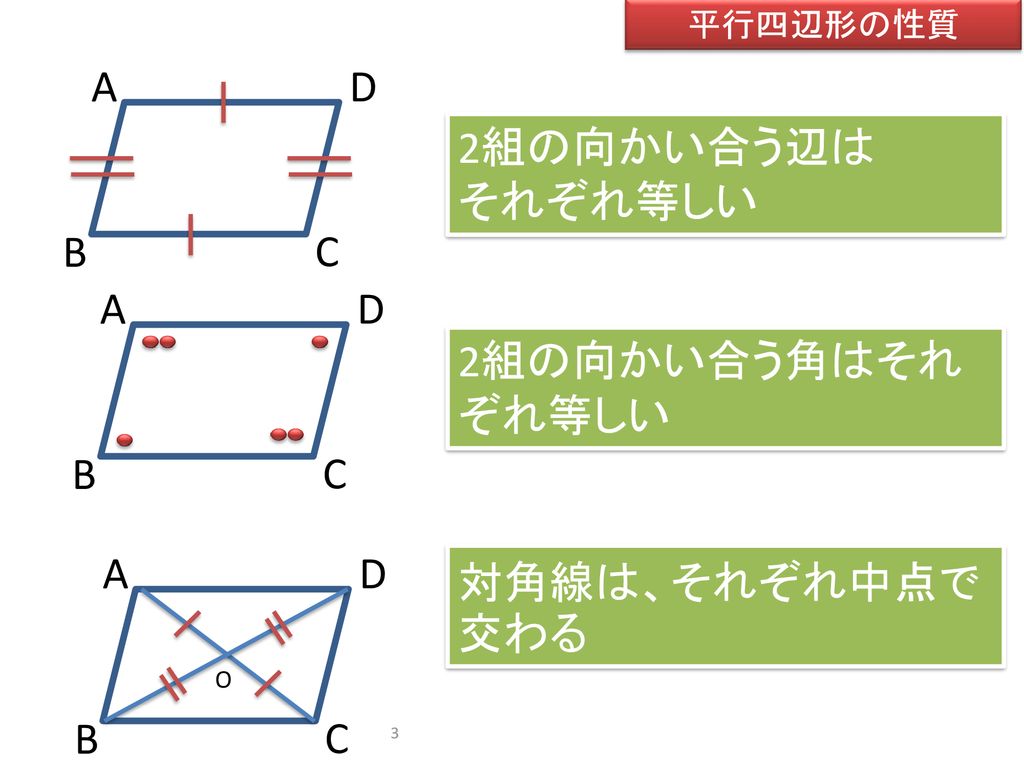
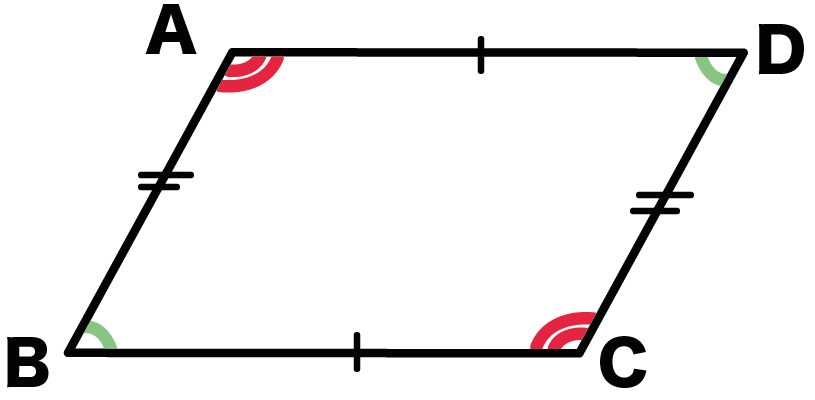
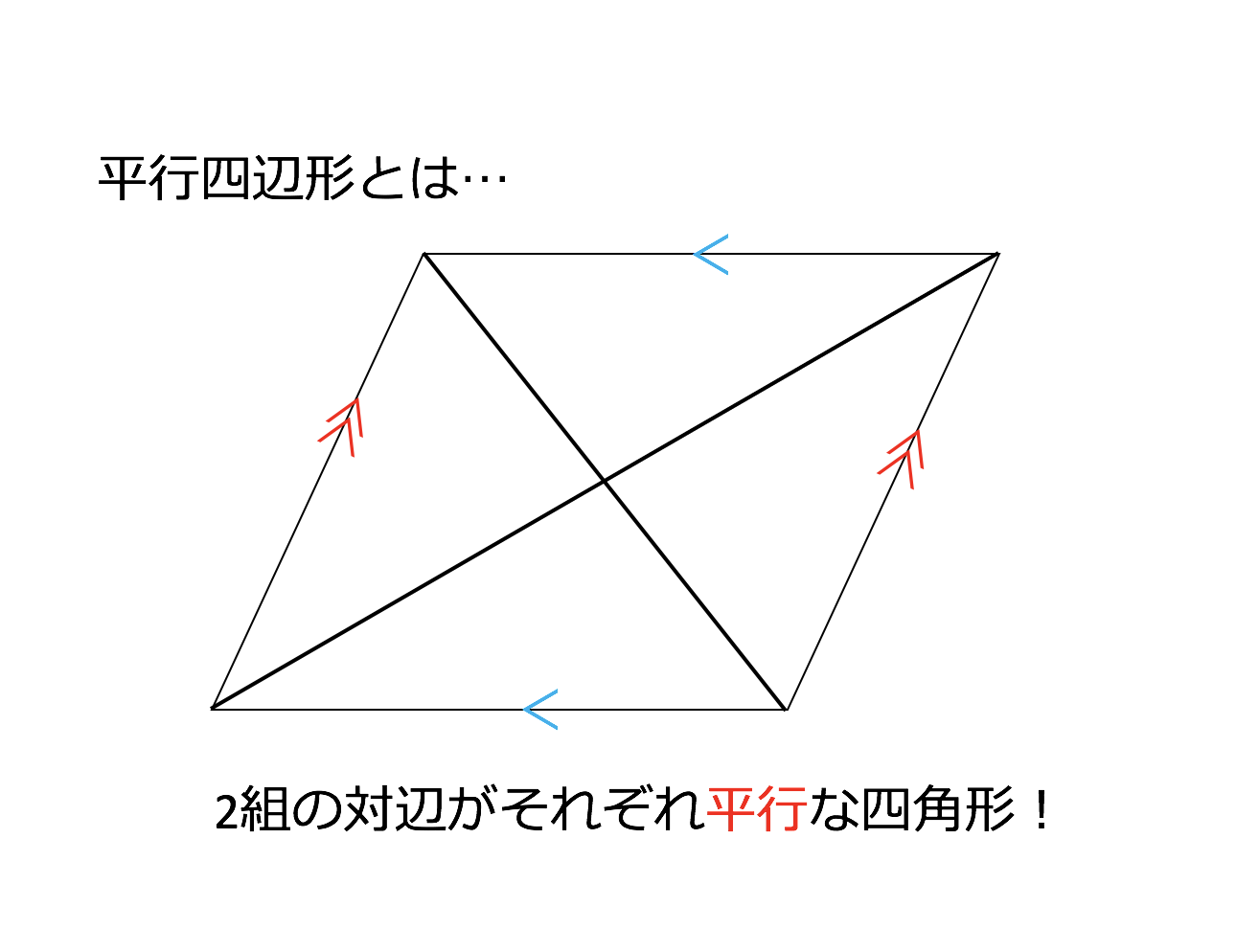
(2) 平行四辺形の性質や平行四辺形であるための条件を見いだし，論理的に確かめることができる。 (3) 平行線を使った等積変形について理解することができる。 (4) 証明した図形の性質を，いろいろな場面で活用することができる。 6 単元の評価規準 数学への平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図） 1 平行四辺形の向かい合う辺は等しい。 （証明） 2 平行四辺形の向かい合う角は等しい。 （証明） 3 平行四辺形の対角線は、それぞれの中点で交わる。 （証明） ＜戻る＞平行四辺形5条件に、さらに厳しい条件を加えると 「長方形」や「ひし形」や「正方形」になりますね！ 「付け加える」ということは、これら3つの図形は それぞれ「平行四辺形の条件」を全て備えているということですね (1) 長方形

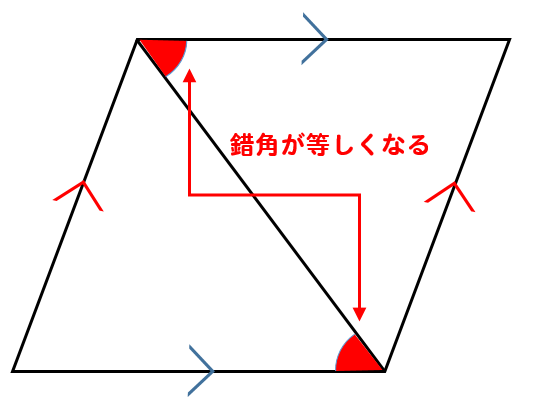
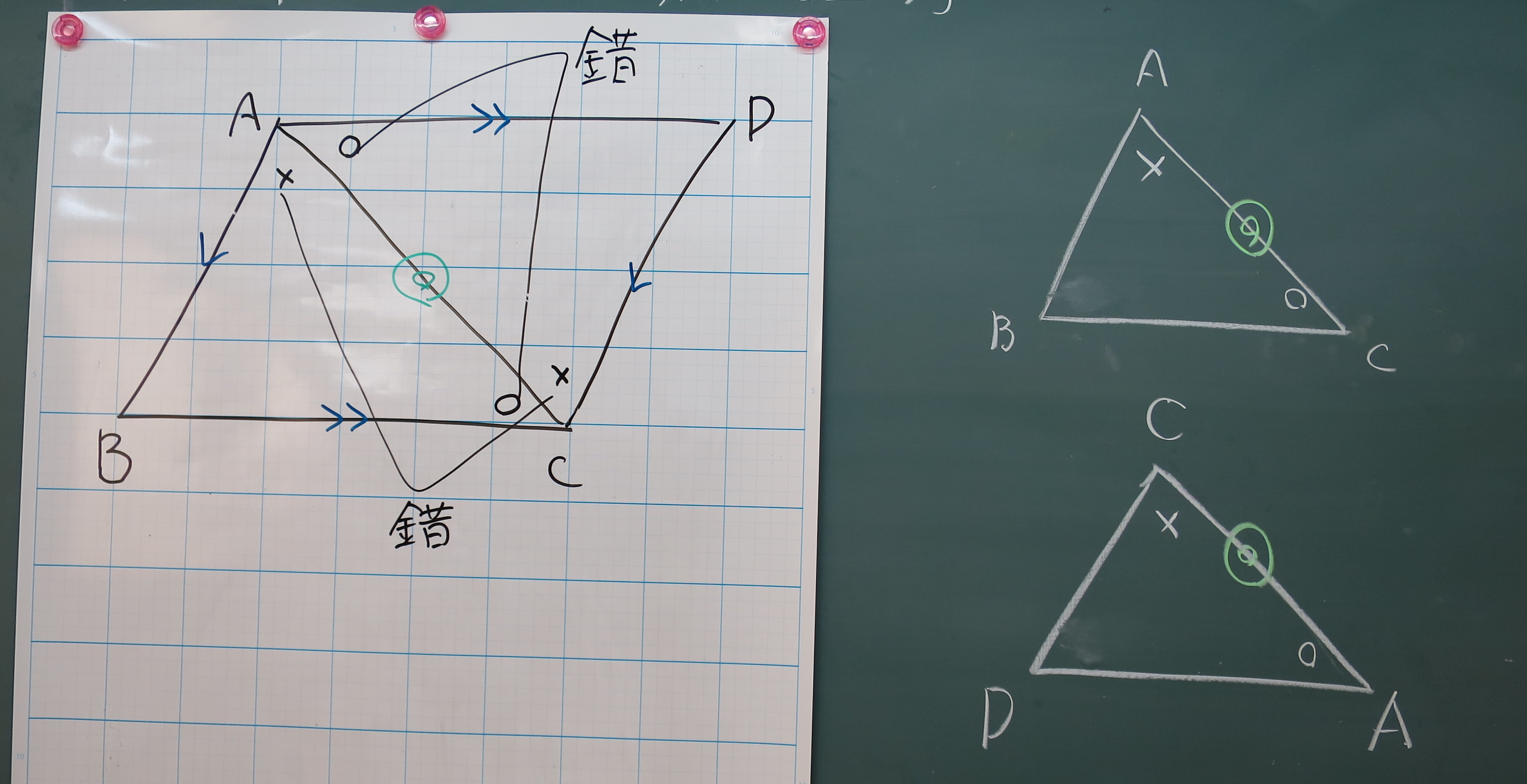
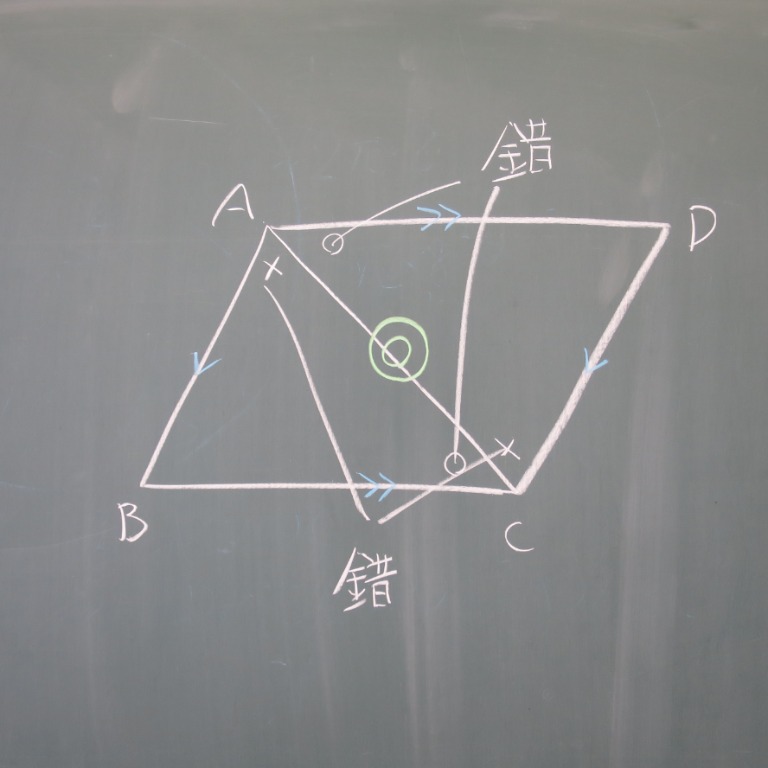
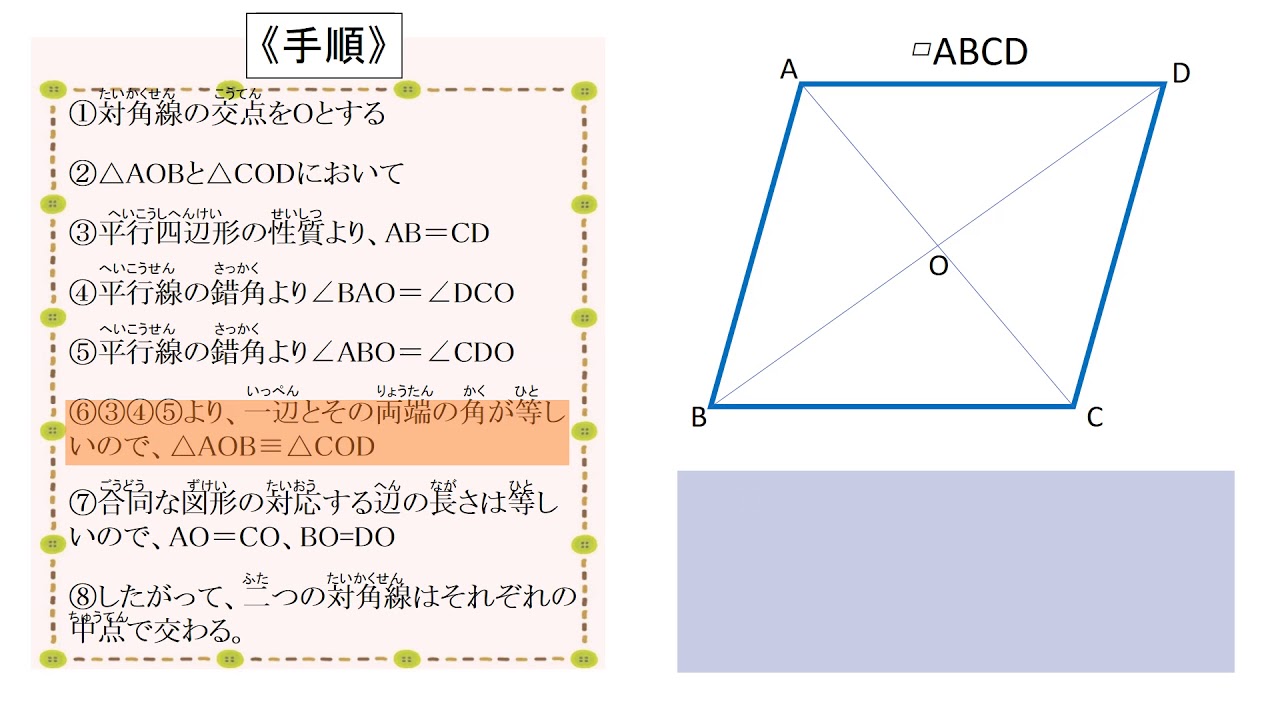
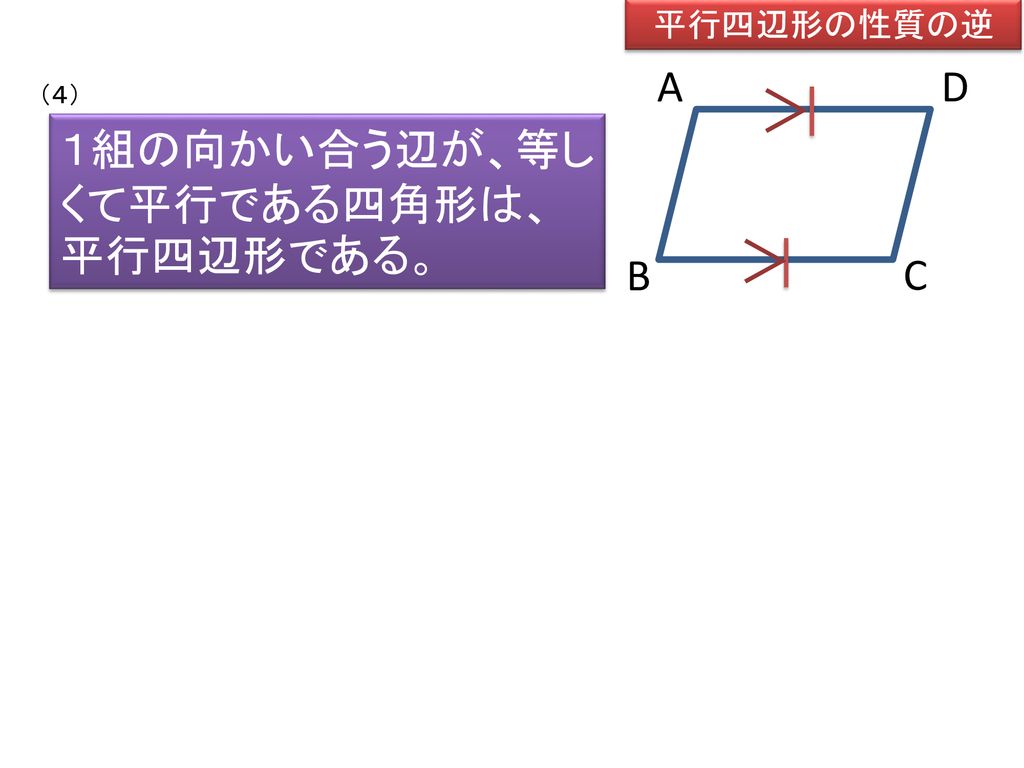
平行四辺形になる条件 平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。 （ 定義 ） 2 2組の向かいあう辺が、それぞれ等しい。 （ 証明 ） 3 2組の向かいあう角が、それぞれ等しい。 （ 証明 ） 4 対角線が、それぞれの中点で交わる。 （ 証明 ） 5 1組の向かいあう辺が、等しくて平行である。 （ 証明 ）平行四辺形は3つの特別な性質がありますが、これらは「四角形の向かい合う2組の辺がそれぞれ平行」ということに由来するものです。 では平行四辺形の性質を定義から証明してみましょう。 平行四辺形の性質の証明 平行四辺形の定義を仮定したとき、それぞれの性質をもつことを証明しましょう。 四角形ABCDにおいて対角線の交点をOとします。 AB//DC、AD//BCのとき、「AB＝DC、AD=BC」2組の対辺が平行ならば、対角線がそれぞれ の中点で交わることの証明 仮定 結論 b c a d ab//cd tab//bc ao=co tbo=do aboと cdoにおいて 平行四辺形の対辺は等しいから ab＝cd ・・・① 平行線の錯角は等しいので ab//cdより ∠abo＝∠cdo・・・② ∠bao＝∠dco・・・③

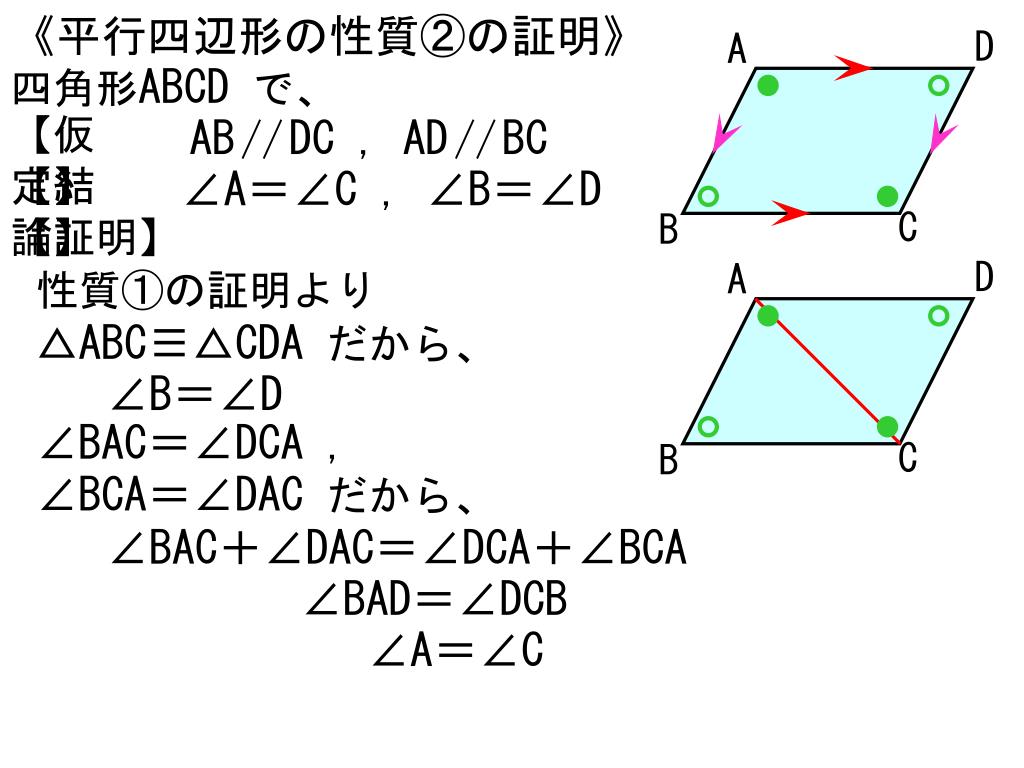
平行四辺形は向かい合う辺が、お互いに平行になっています。 平行になっているという性質を知っておくと このように錯角が等しくなる ということも利用できるようになりますね。 2組の対辺はそれぞれ等しい 平行四辺形は、向かい合う辺がそれぞれ等しくなります。 2組の対角はそれぞれ等しい 平行四辺形の向かいあう角は、それぞれ等しくなります。 ここで、もう一つ覚えておくと得なのが 平平行四辺形の性質 平行四辺形は、次のような性質を持つ。 対辺の長さが等しい（対辺は2組あるが、いずれもこの性質を満たす）。 対角の大きさが等しい（対角は2組あるが、いずれもこの性質を満たす）。 対角線 が他の対角線の 中点 を通る（対角線は2本あるが、いずれもこの性質を満たす）。 平行四辺形は、 点対称 な図形である。 対称の中心は、対角線の交点に等しい。 平行四辺形の対角線に2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。

テボールの定理 雑学のソムリエ

平行四辺形になることの証明 Youtube

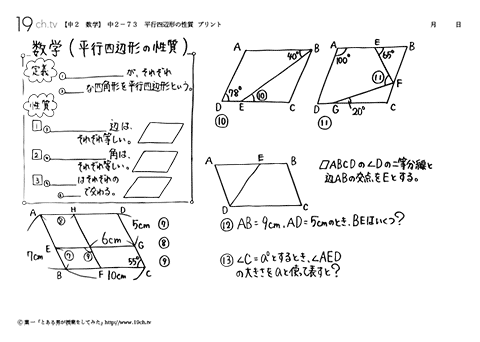
平行四辺形（2 時間） 図 〈目標〉 平行四辺形の性質について調べ，既習内容をもとに平行四 辺形の性質について考察し，理解す ることができ。 問題 のように トイレッ ペーパーを重ねます。 AB＝12cm，BC＝24 xとy の値を求めなさい。 平行四辺形の性質 こんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定小学4年生の算数 台形・平行四辺形・ひし形・対角線 問題プリント 立方体練習問題プリントを無料ダウンロード・印刷できます。直方体・立方体の概念と性質、展開図や見取図のかき方、 面や辺の平行・垂直の関係、2次元座標を使った位置の表し方

平行四辺形の性質 まなびの学園

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

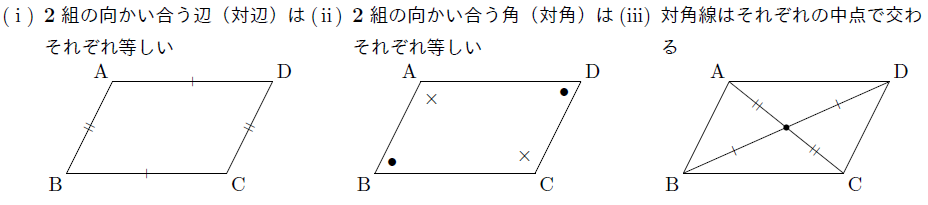
(1) このとき，平行四辺形の2 組の向かい合う辺の長さは 等しいことを証明せよ。 (2) (1)を使って，平行四辺形の対角線は中点で交わること を証明せよ。 解答欄 (1) 平行四辺形の性質（定理） 平行四辺形には、大きく つの性質があります。 性質①2 組の向かい合う辺の長さが等しい 性質②2 組の向かい合う角が等しい 性質③2 本の対角線が中点で交わる 以上の つです。 言葉だけで覚えるのは難しいと思うので、図とともに理解しながら覚えておきましょう。 平行四辺形の条件 ある平面図形が平行四辺形であるための条件には、次の つが平行四辺形の性質 パワーポイント教材(348k) ワークシートパック 平行四辺形になる条件 パワーポイント教材(163k) ワークシートパック 平行線と面積 パワーポイント教材(292k) ワークシートパック 5章 章末問題 パワーポイント教材(k)

中学2年の数学 動画 平行四辺形の性質の問題 19ch

無料 中２数学 基本解説 解答プリント 230 平行四辺形１ 性質

 平行四辺形の定義は、2組の対辺がそれぞれ平行である。 性質・定理 性質というのは、その言葉が持っている特徴のこと。 平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理：1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる条件ばかり平行四辺形の性質（中学数学）のポイントは！ 平行四辺形とは「 2 組の対辺がそれぞれ平行」な四角形のこと 平行四辺形の性質は 3 つ 2 組の の平行四辺形になる条件をみたしているからね。 だから、ひし形である以上、 そいつは平行四辺形でもあるわけだ。 でもね、 平行四辺形はひし形とはいえないよ。 だって、 平行四辺形っていうだけじゃ4つの辺が等しくはないからね。 たとえるなら、

3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

2 64 第４章 平行四辺形 平行四辺形の性質を使った証明 プログラミングの雫

1 単元名 垂直・平行と四角形「四角形をつくろう」 2 単元とその指導について (1) 教材観 本単元では，以下の3点をねらいとしている。 ① 垂直，平行や台形，平行四辺形，ひし形の性質について調第5章 図形と合同 ＜前： L38 平行四辺形の性質 の問題 L39 平行四辺形になる条件 の問題 ：次＞ ※証明の方法は、以下の解答の他にも色々あるかもしれないよ！ 他の方法を見つけるのもとても勉強になるので、ぜひ探してみてね！ 練習問題1 右図の 平行四辺形とひし形って何がちがうんですか？ひし形は対角線が垂直に交わるんでしたっけ？水色のやつなのですが、これはひし形だそうです。でも平行四辺形にも見えますよね？！( _ ;)中3の数学のプリン トです。 ひし形は平行四辺形の種類の一つと考えます。平行四辺形とは、2組の

3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン

平行四辺形は2本の対角線がそれぞれの真ん中で交わります。 長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については 長方形 が 『対角線の長さが等しい』 、 ひし形 が 『対角線が直交する』 という性質があります。 そして正方形は平平行四辺形の性質を利用した証明 平行四辺形の内外にある三角形の合同を証明する問題もあるよ。三角形の合同条件を改めて確認しておこう。 （1）3辺がそれぞれ等しい。 （2）2辺とその間の角がそれ平行四辺形の性質 向かい合う辺がそれぞれ平行 向かい合う辺がそれぞれ等しい 向かい合う角がそれぞれ等しい 対角線がそれぞれの中点で交わる 更に、これに加えて ひし形の性質 すべての辺が等しい 対角線が垂直に交わる という性質も持っています。 覚えておいてください (^^) 平行四辺形とひし形の面積 ひし形は平行四辺形の仲間と言いましたが、面積を求める公式は別々で覚えておき

平行四辺形の3つの性質とその証明 具体例で学ぶ数学

3

平行四辺形 平行四辺形の定義 2組の対辺がそれぞれ平行な四角形 平行四辺形の定義からつぎの性質を導くことができる 2組の対辺はそれぞれ等しい。 >>証明 2組の対角はそれぞれ等しい。 >>証明 対角線はそれぞれの中点で交わる。 >>証明 例 平行四辺形の上の3つ以外の性質として、 「平行四辺形は点対称な図形」 というものがあります。 点対称とは図形を回転させても同じ図形になるようなもののことをいいます。 また、対称の中心 (回転の軸)は、 対角線の交点 (中点) に等しいということも特徴の1つです。 平行四辺形の面積 (公式・証明) 平行四辺形の 面積の求め方 についてです。 平行四辺形の面積は、 「底辺×高さ

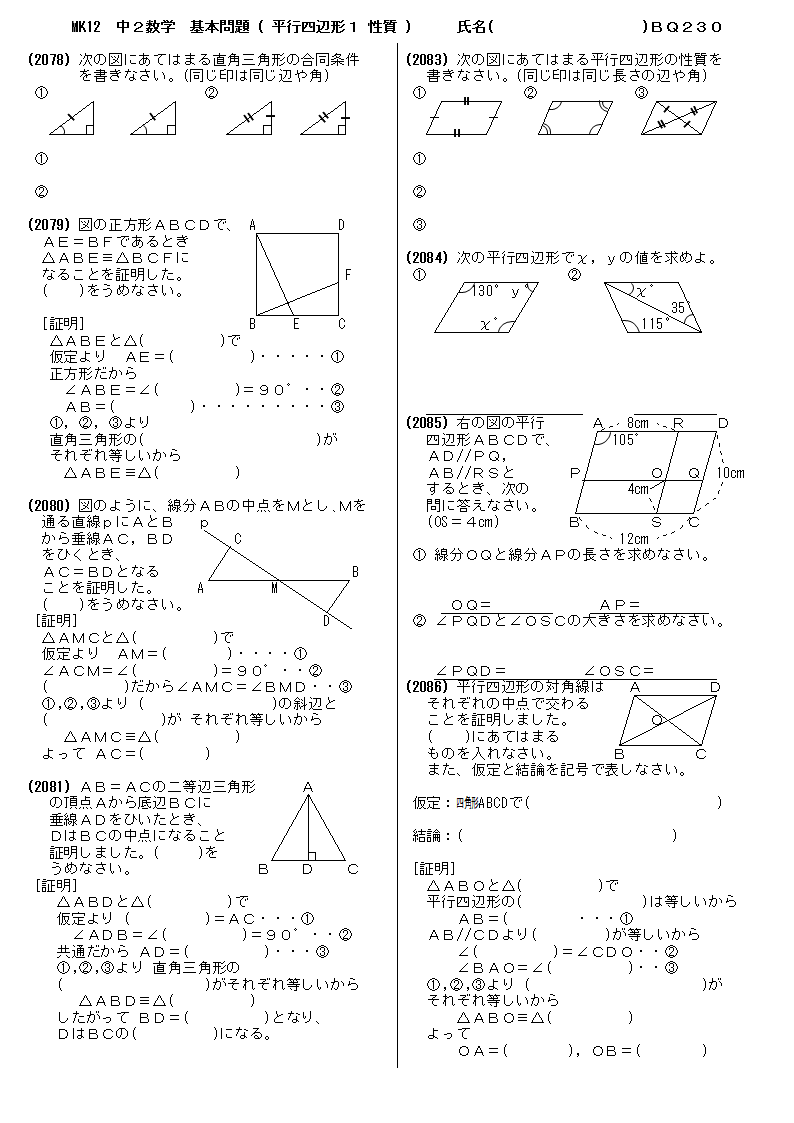
無料 中２数学 基本問題 問題プリント 230 平行四辺形１ 性質

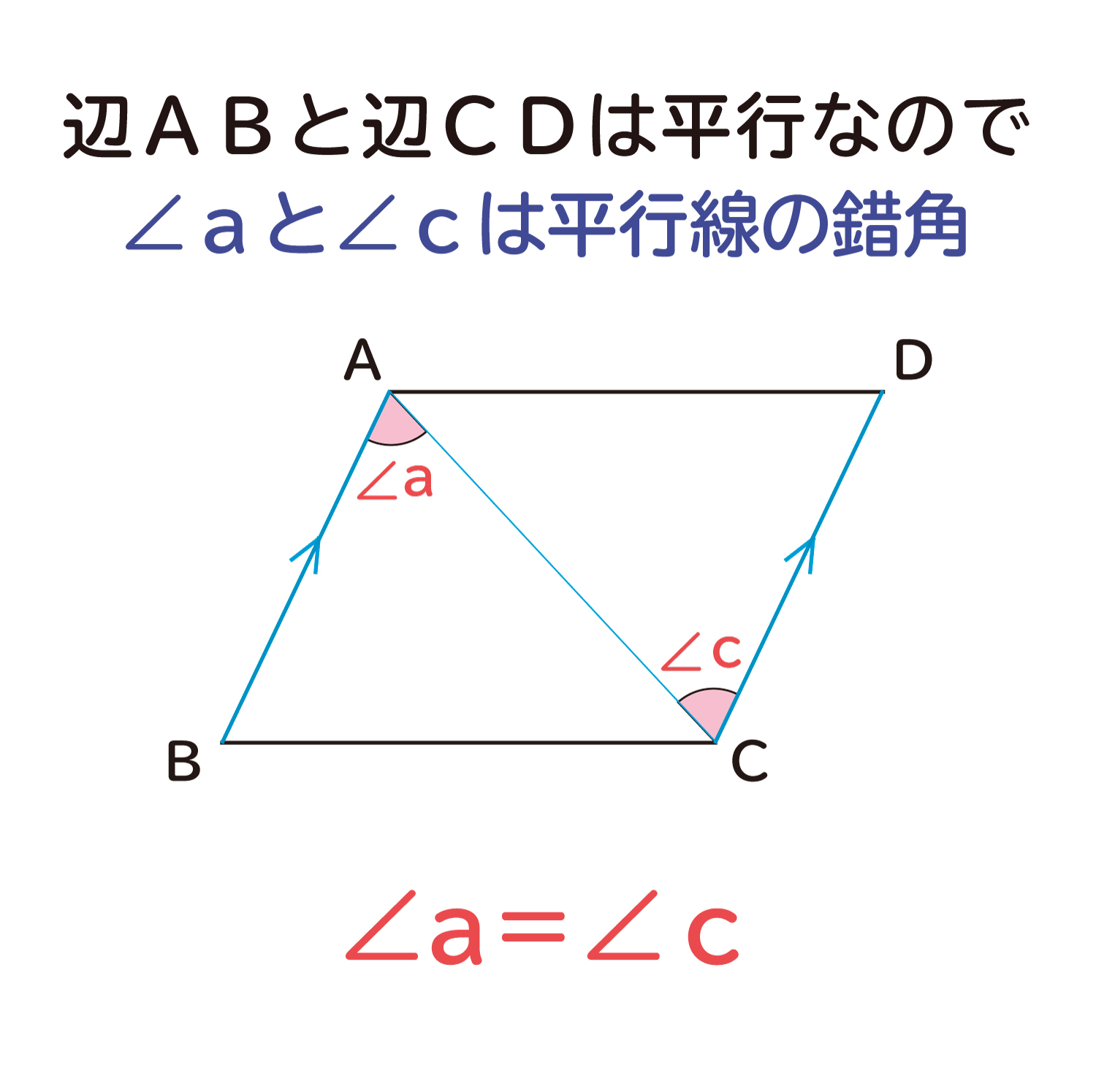
平行四辺形の対辺の長さは等しくなる ことの説明 おかわりドリル

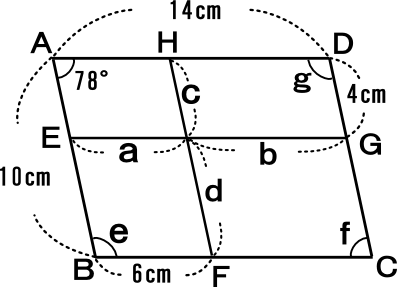
中学２年数学練習問題 図形と合同 平行四辺形の性質と証明問題

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

Tossランド 平行四辺形の性質

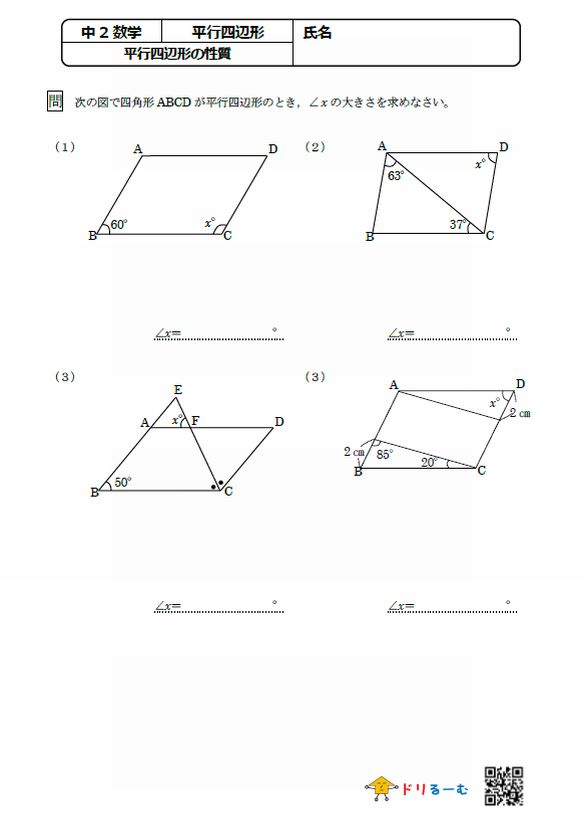
平行四辺形の性質 ドリるーむ

平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

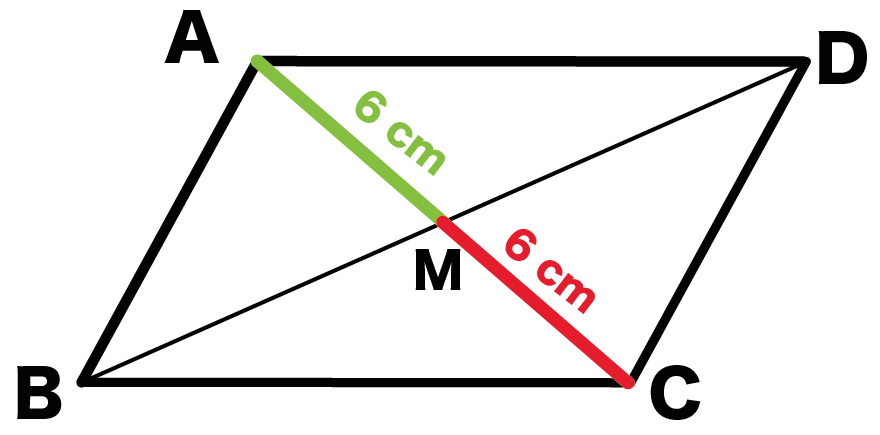
中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく

平行四辺形の定義と性質 証明問題の解き方 数学fun

関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

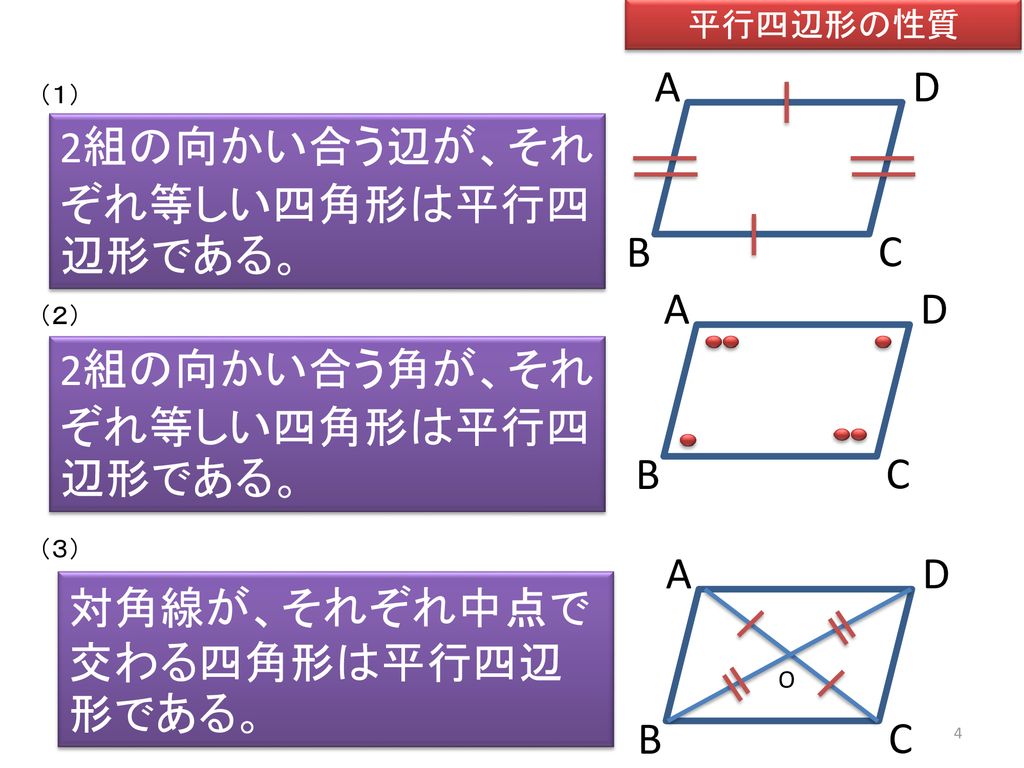
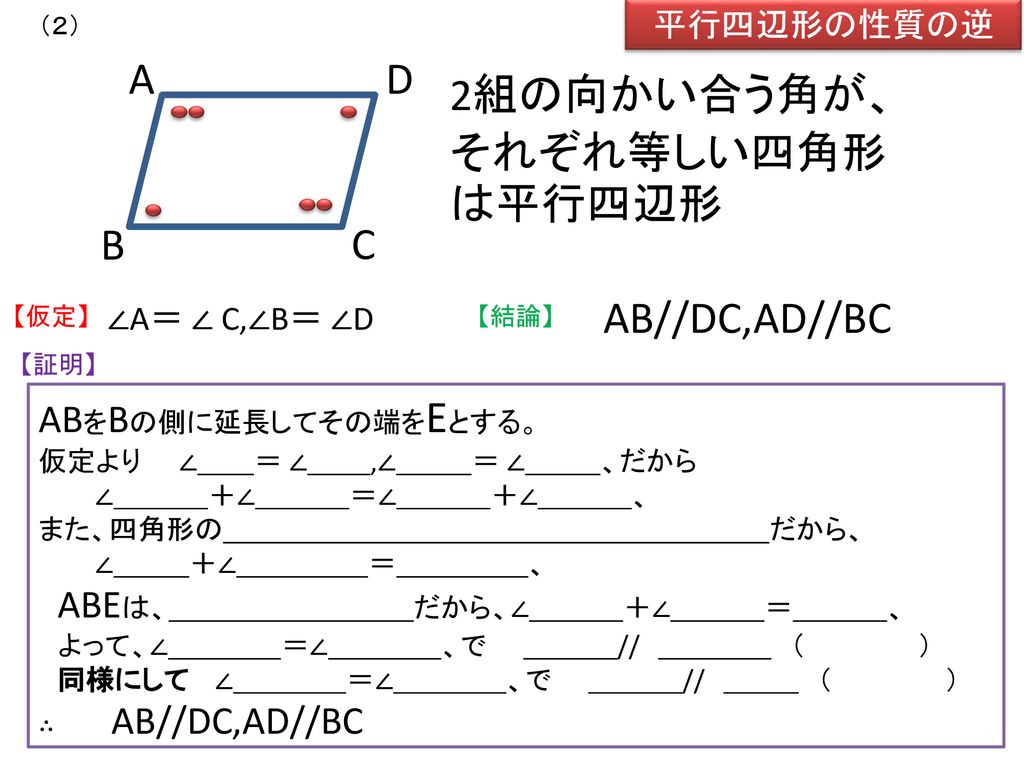
平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

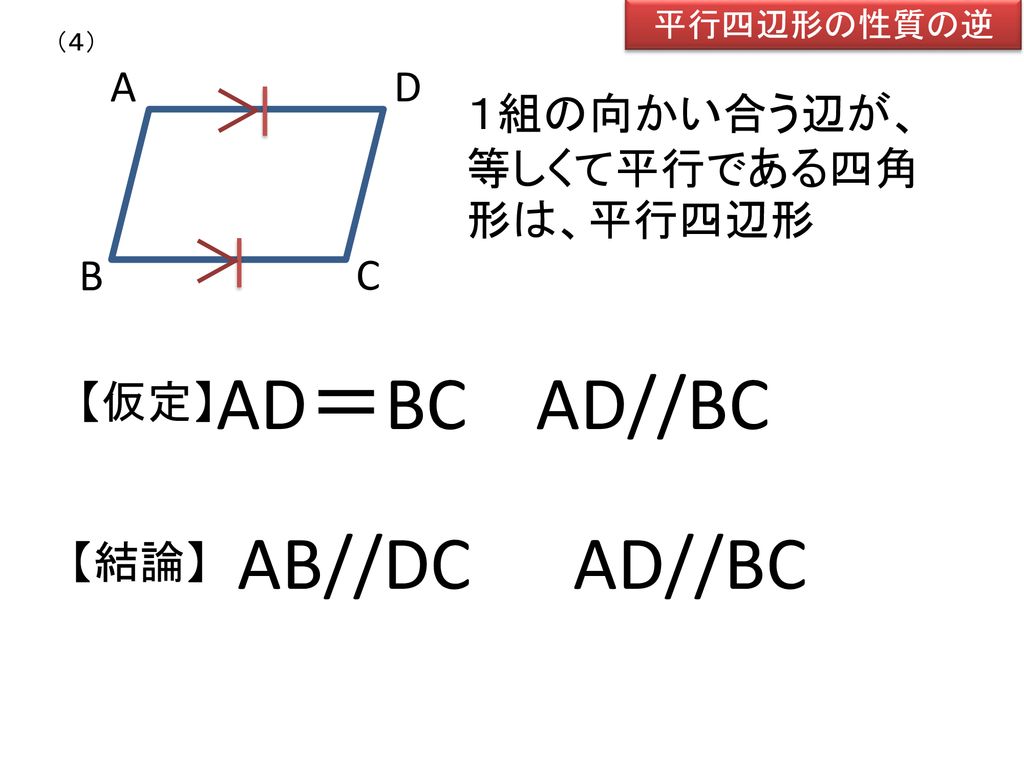
平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

Tossランド 平行四辺形の性質

平行四辺形の性質を全部教えてください Clearnote

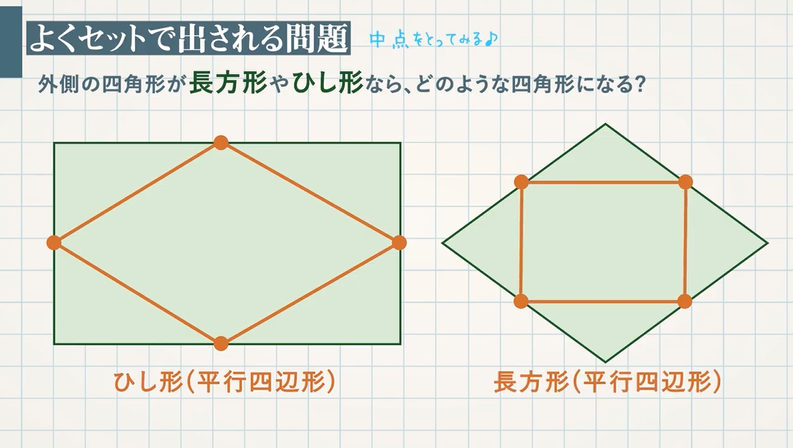
中点連結定理を使った平行四辺形であることの証明 教遊者

平行四辺形の辺や角を求める Youtube

中2 平行四辺形の性質 日本語版 Youtube

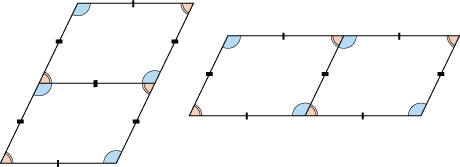
平行四辺形の性質 ５年生 算数の広場

簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

平行四辺形の性質の証明 中学数学教材研究ノート

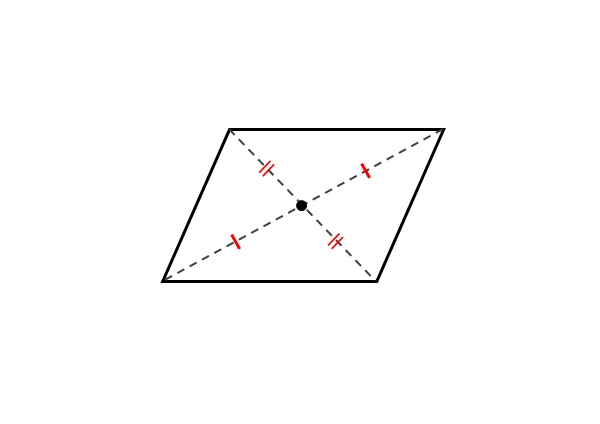
図形と方程式 平行四辺形の頂点の座標について 日々是鍛錬 ひびこれたんれん

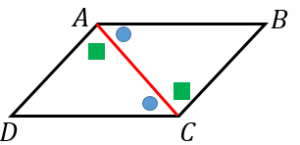
平行四辺形の3つの性質とその証明 具体例で学ぶ数学

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

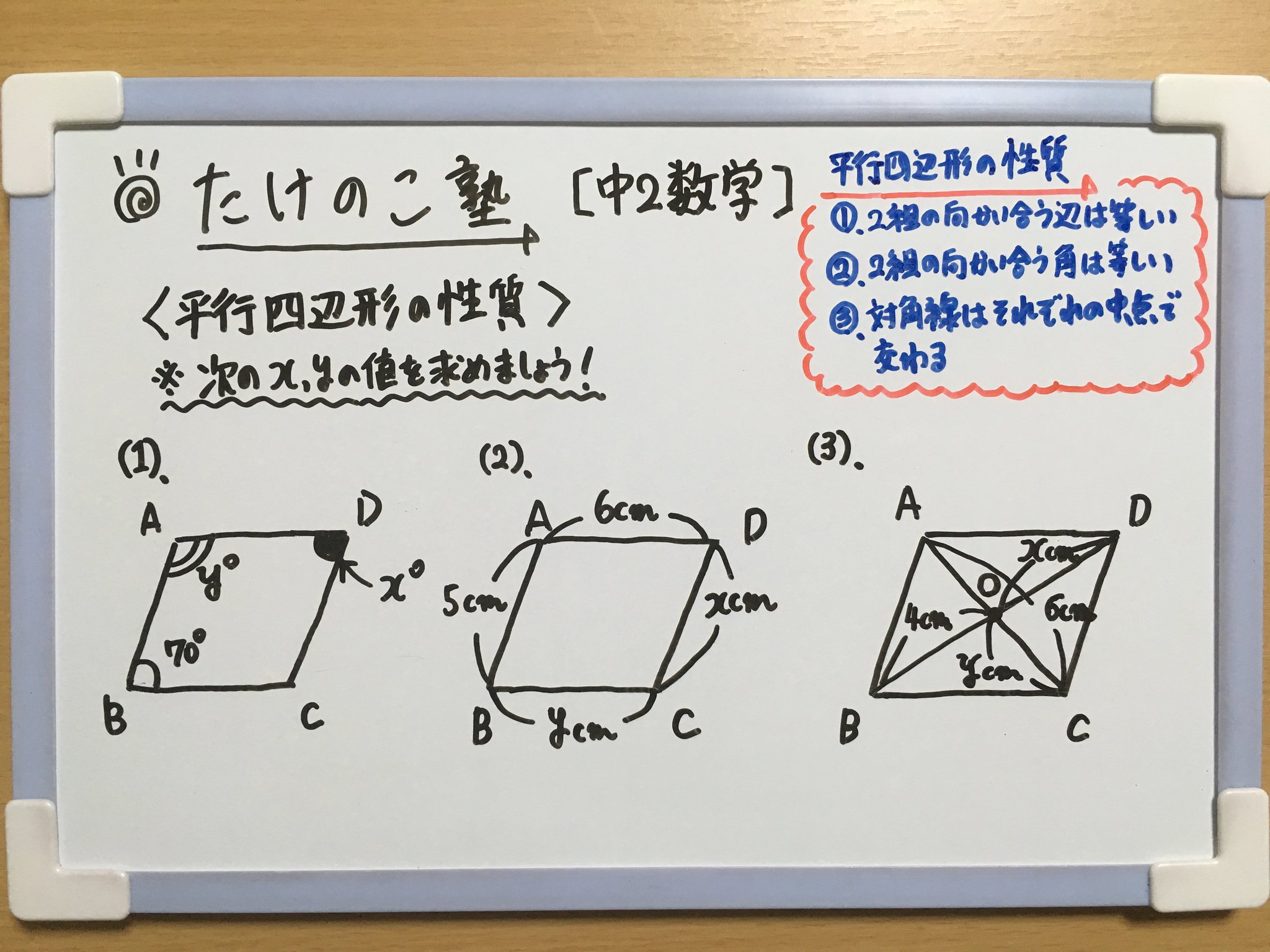
O Xrhsths たけのこ塾 Sto Twitter 今回は 平行四辺形の性質 を作成しました 平行四辺形の性質 2組の向かい合う辺は等しい 2組の向かい合う角は等しい 対角線はそれぞれの中点で交わる 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学 平行四辺形

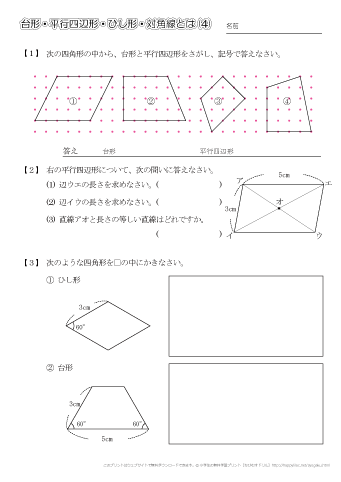
小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく

数学 中2 73 平行四辺形の性質 Youtube

Math 平行四辺形 平行四辺形になることの証明 働きアリ

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

平行四辺形の性質

中2数学 平行四辺形の証明のポイントと練習問題 Examee

中2 平行四辺形の性質の証明3 対角線 日本語版 Youtube

ネムネコの部屋 第４回 平行四辺形の性質

1

小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

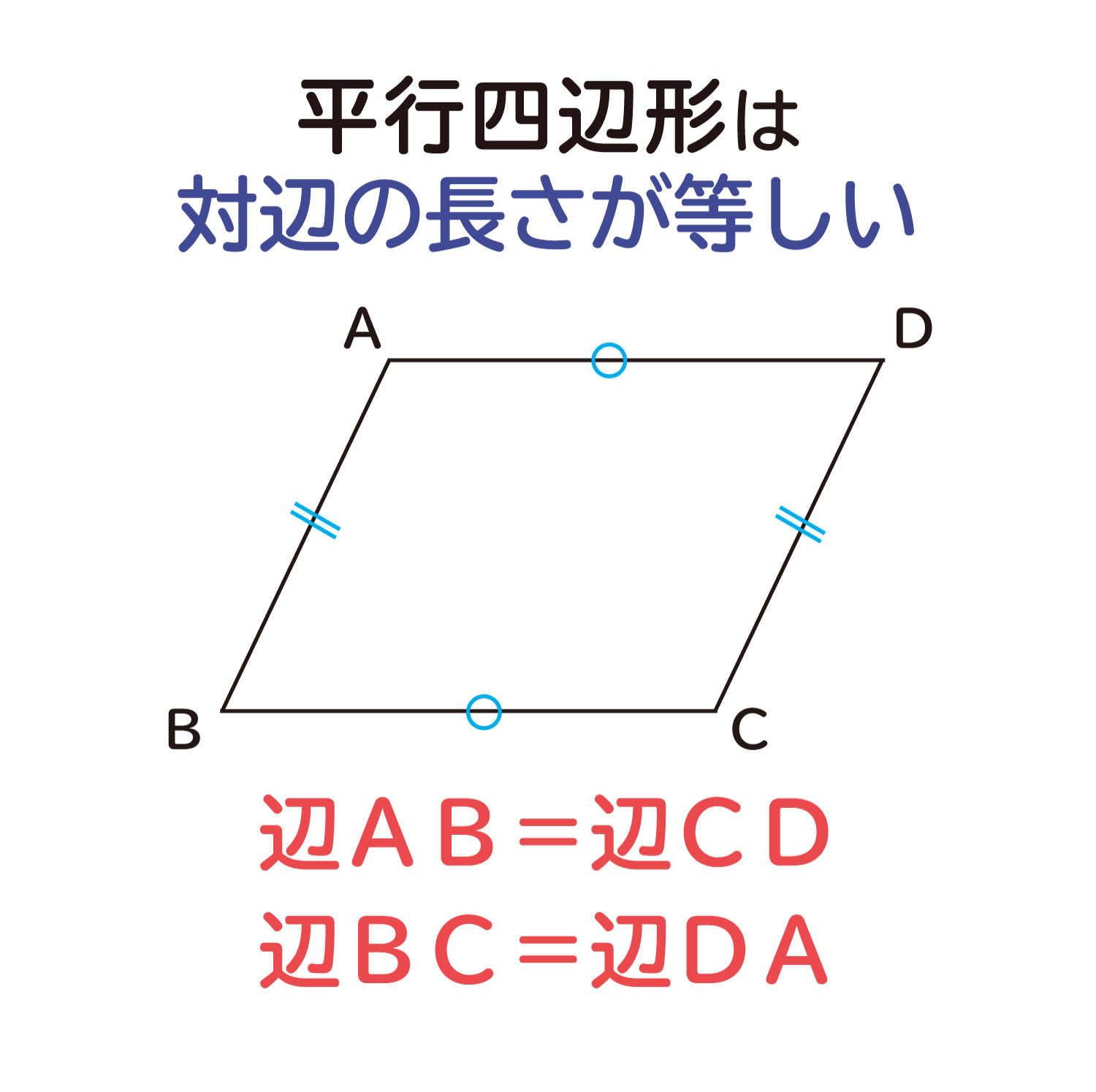
平行四辺形の対辺の長さは等しくなる ことの説明 おかわりドリル

平行四辺形 中学数学で遊ぶ 身勝手な主張

高校入試 英語 数学 学習 三角形と四角形 平行四辺形

Ppt ５ 図形と合同 Powerpoint Presentation Free Download Id

四角形の性質 ひし形の性質 平行四辺形の性質 正方形の性質 長方形の性質 女子学院中学 05年 平成17年度 入試算数問題 まいにち一題 中学受験過去問題研究

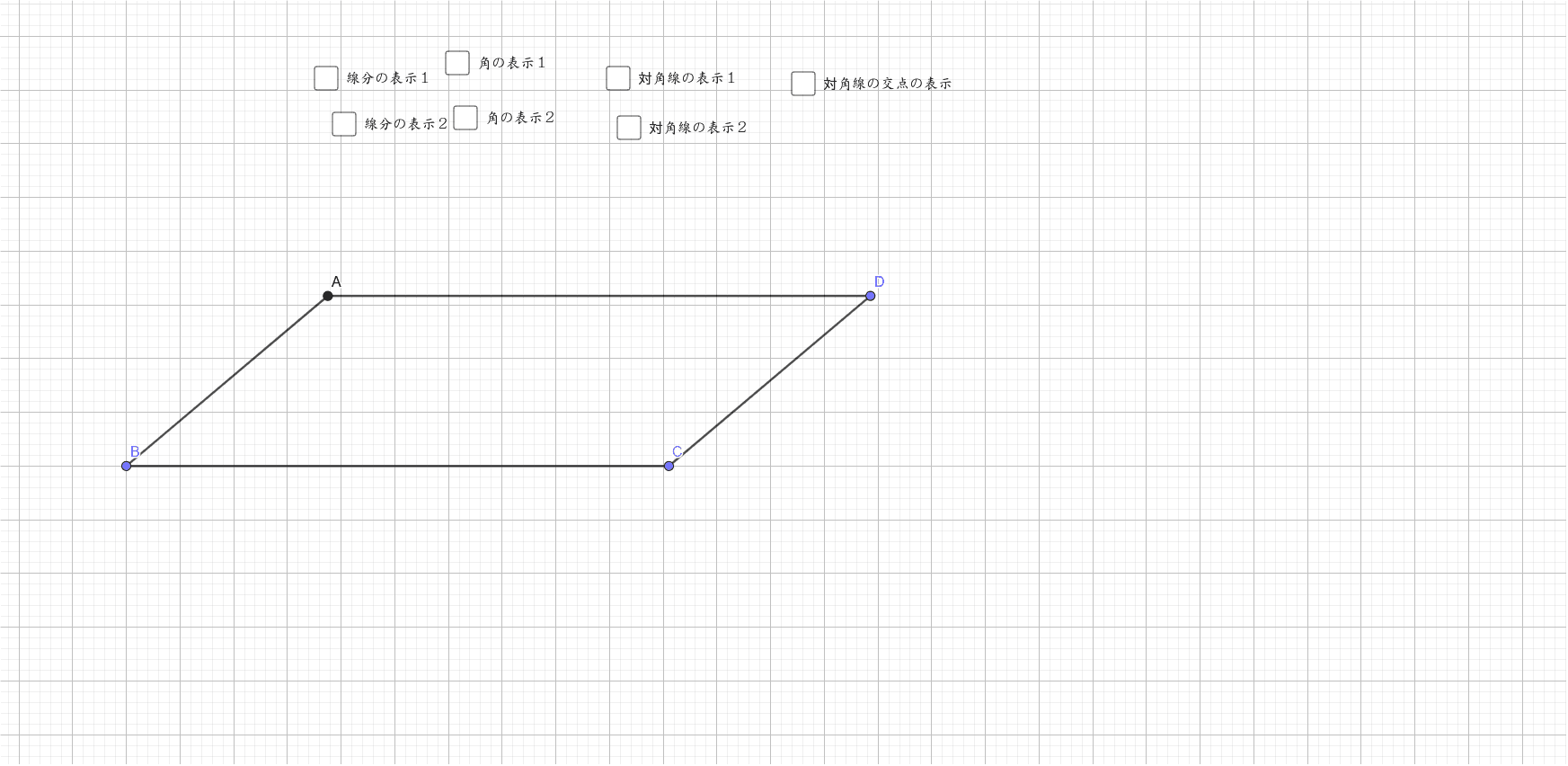
Test 平行四辺形の性質 Geogebra

3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

中2 授業ノート 平行四辺形の性質 中学生 数学のノート Clearnote

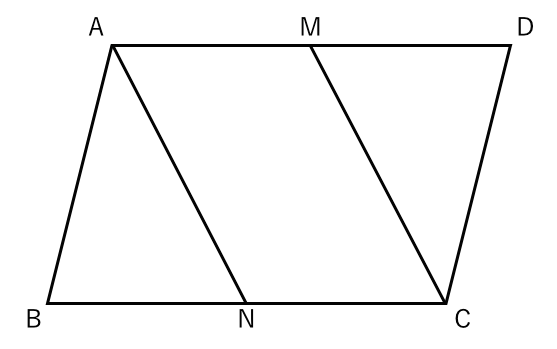
平行四辺形であることを証明する 苦手な数学を簡単に

平行四辺形について知ろう 苦手な数学を簡単に

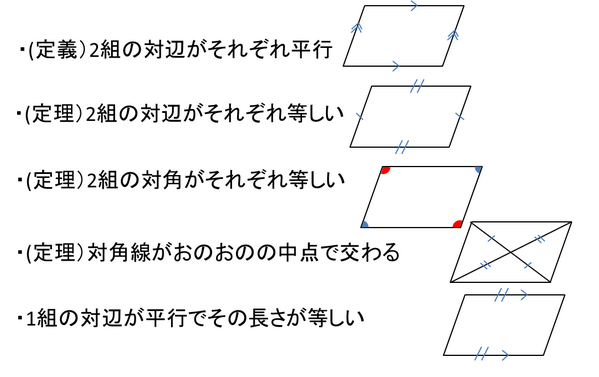
140字で高校受験 数学 平行四辺形の定義 性質 なるための条件 言葉だけでなく図で覚える T Co Amwmvf58n7

1

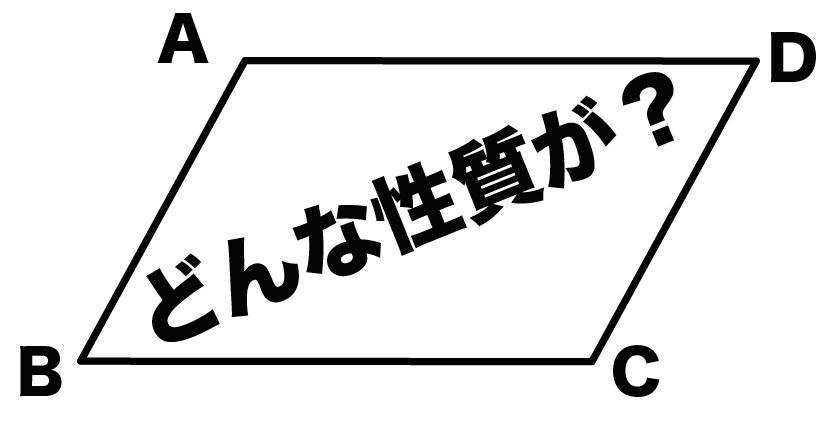
中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく

平行四辺形の性質1

中学２年数学 平行四辺形の性質 練習問題５ あんのん塾

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clearnote

1

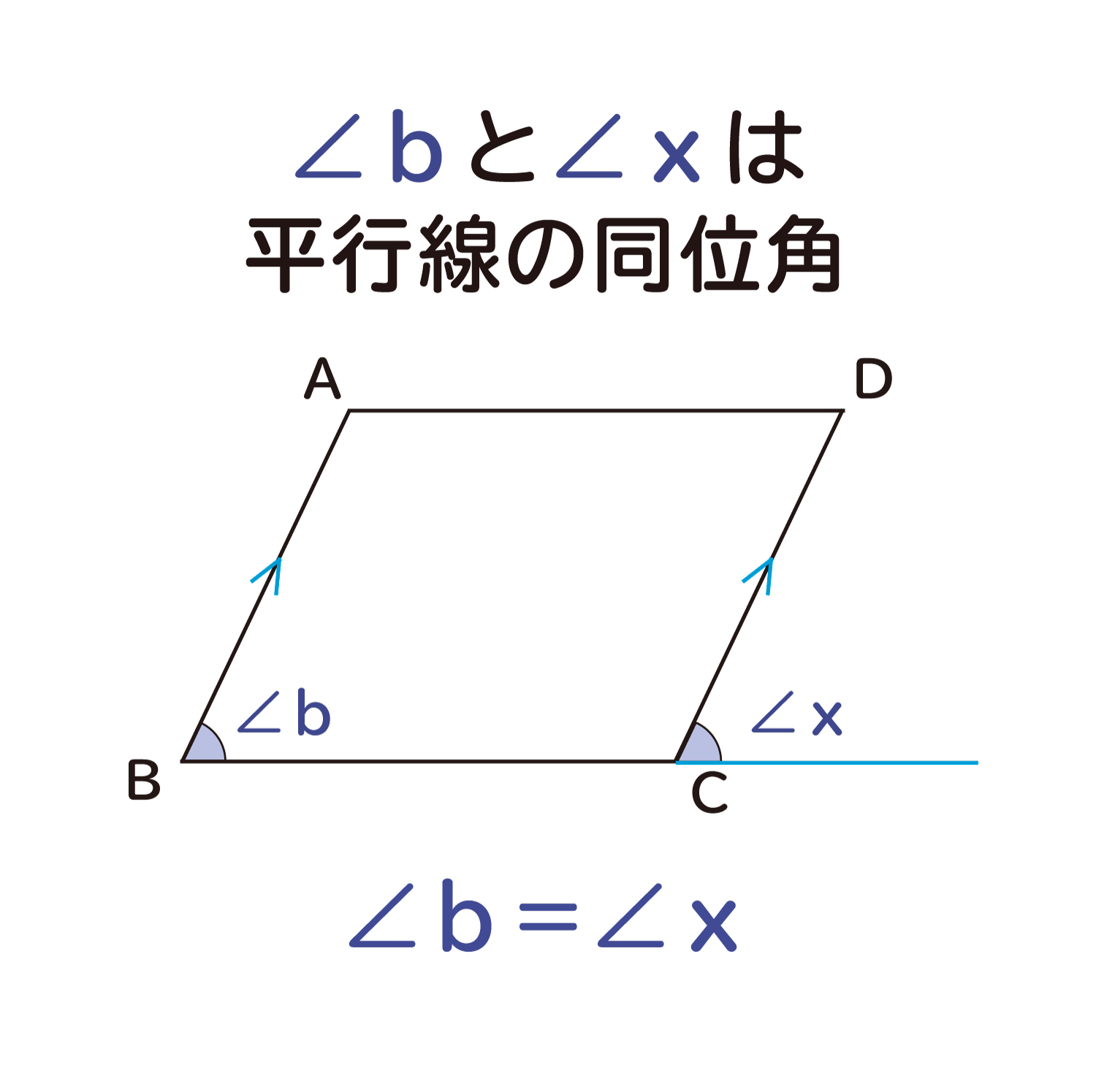
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学

平行四辺形の性質

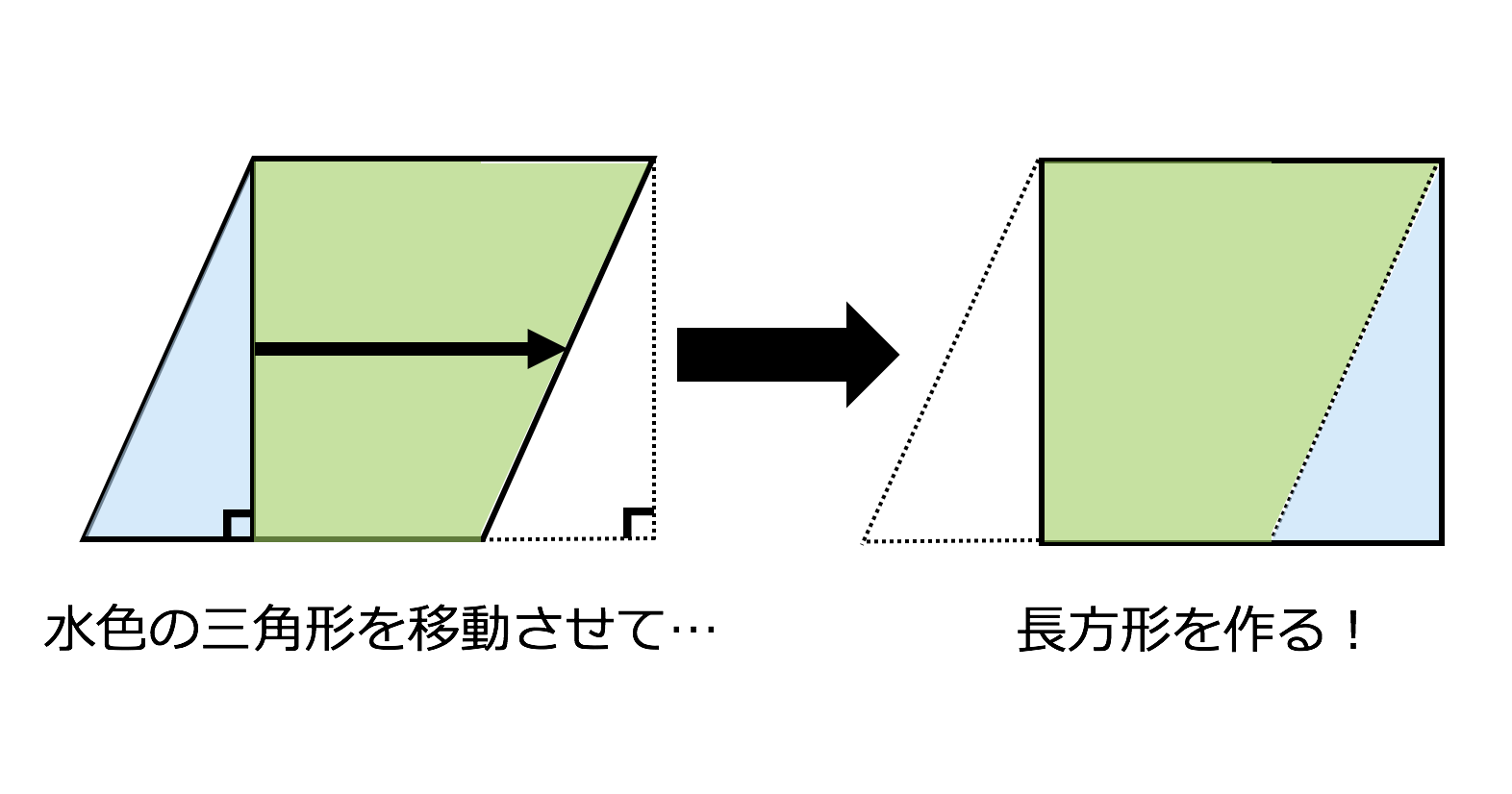
3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント

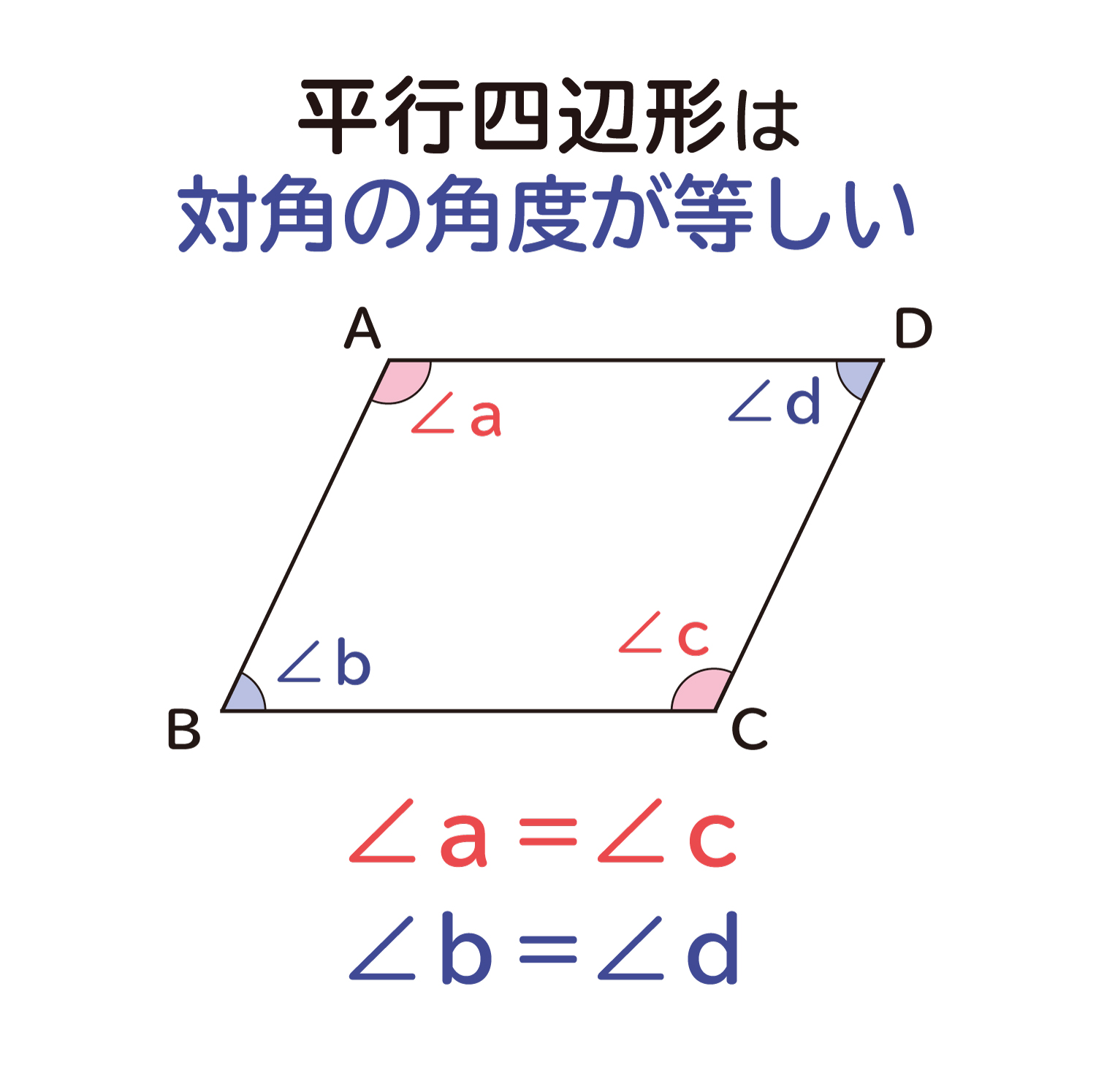
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学

2 63 第４章 平行四辺形 平行四辺形の性質 ニュージーランド短期留学ダイアリー

中2数学 平行四辺形の証明の定期テスト予想問題 Pikuu

平行四辺形の性質

平行四辺形の性質 と ひし形の性質 を比べる とちぎｅライブラリ

平行四辺形になる条件 小学生 中学生の勉強

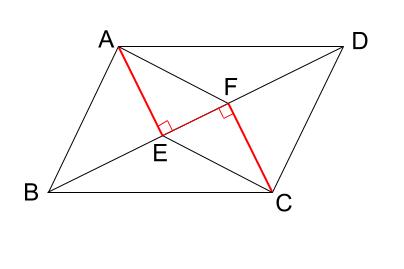
中学数学 平行四辺形になることの証明 その２ 中学数学の無料オンライン学習サイトchu Su

中2数学 平行四辺形の性質 練習編 映像授業のtry It トライイット

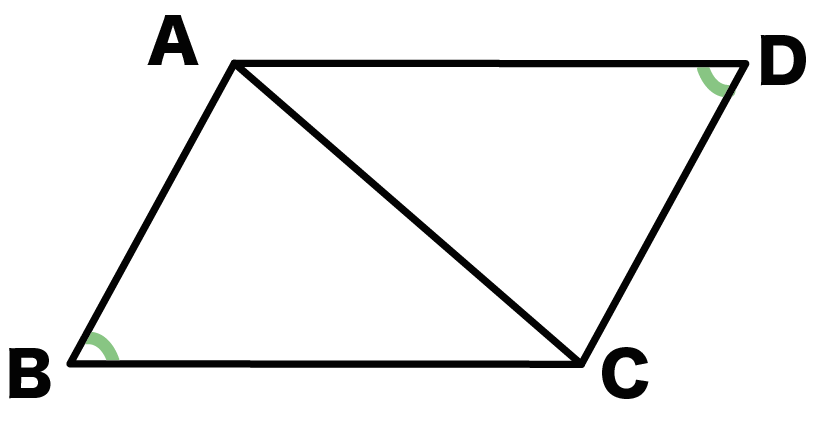
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく

平行四辺形 Wikipedia

中2数学 平行四辺形の性質の利用 例題編 映像授業のtry It トライイット

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

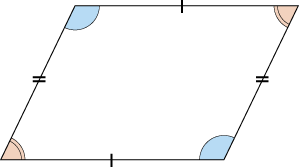
平行四辺形の性質 ５年生 算数の広場

平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

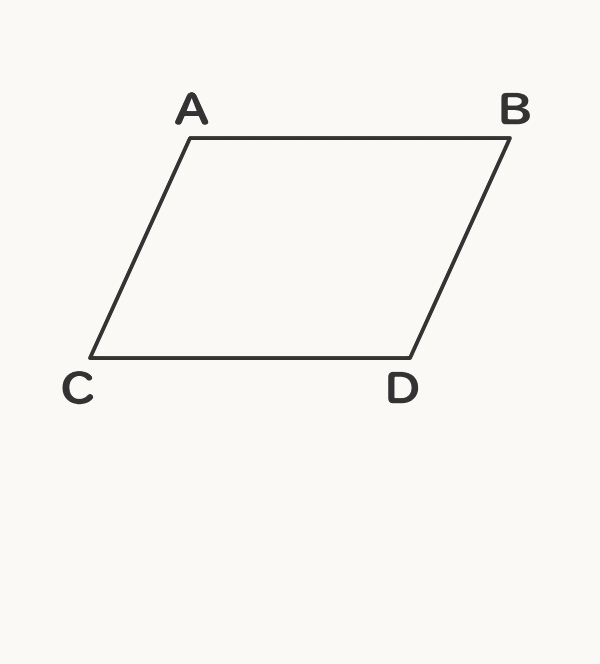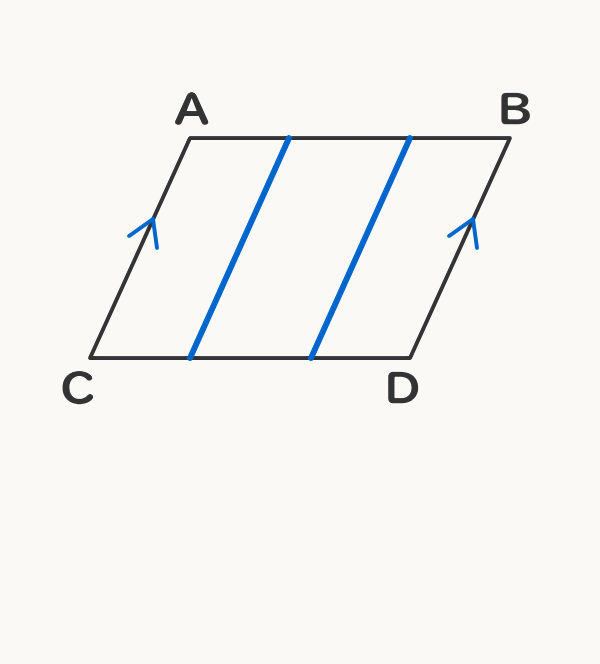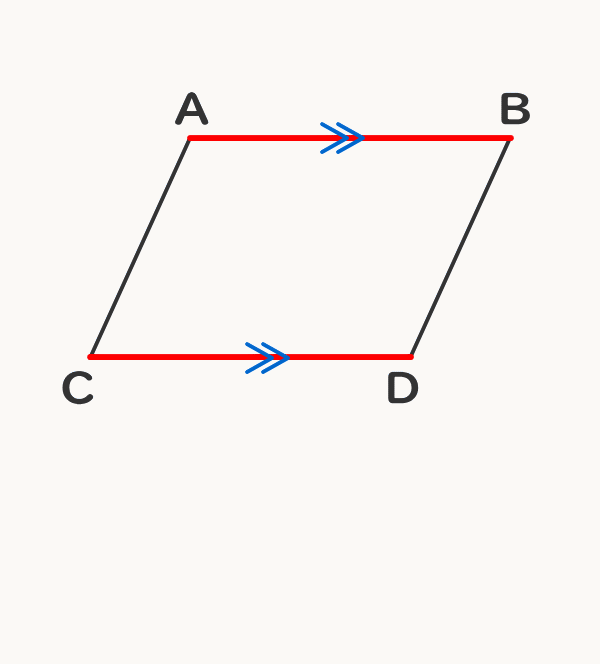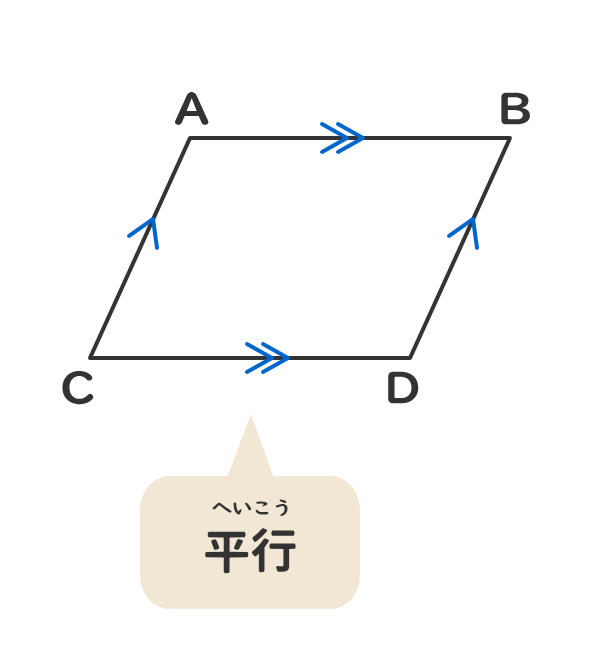
平行四辺形の仲間を知ろう 電験3種web

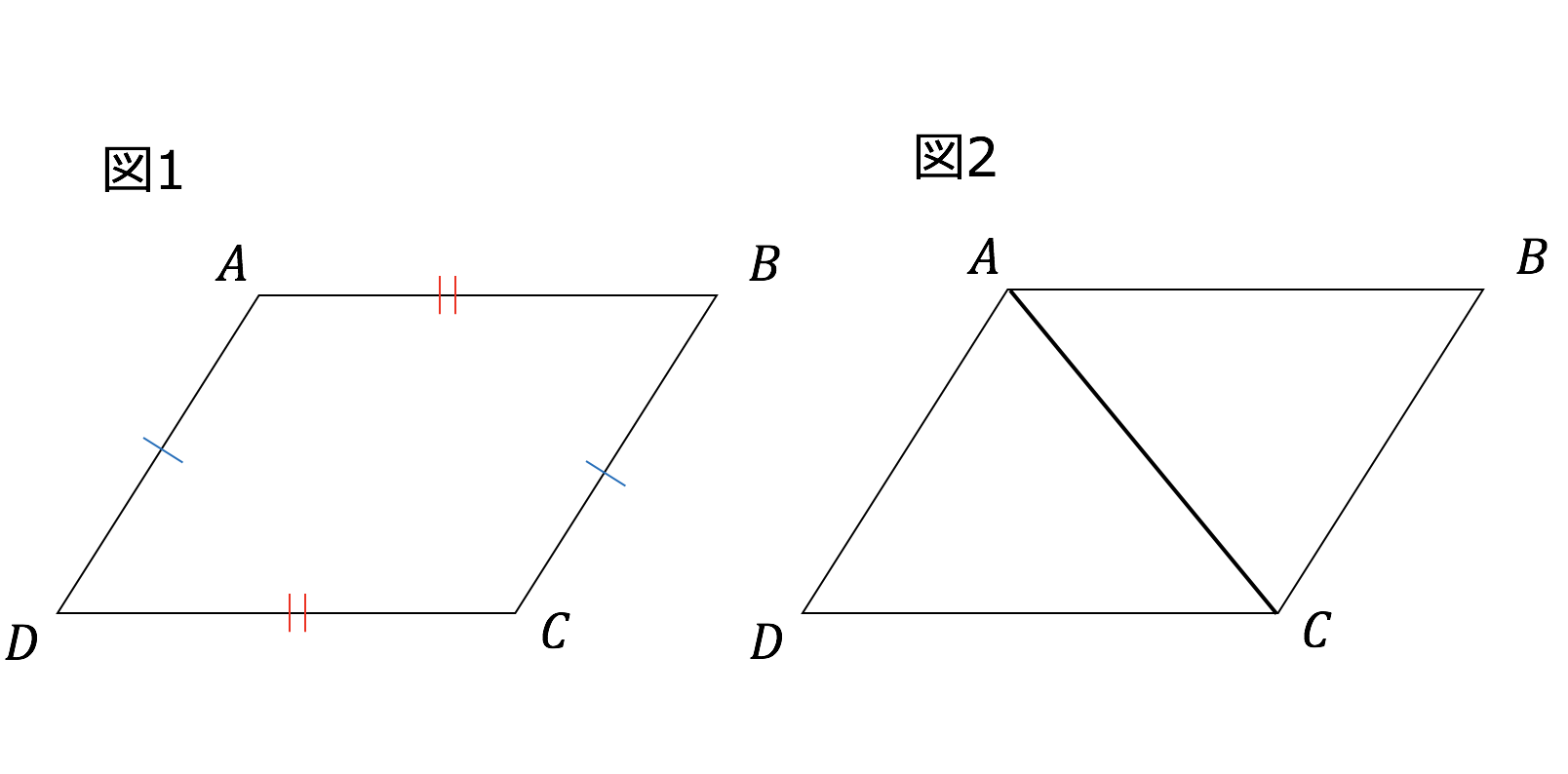
3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

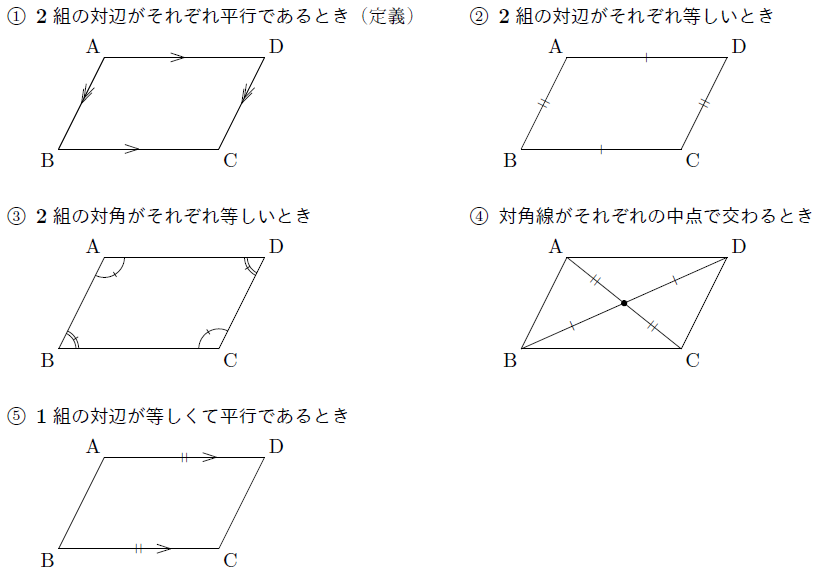
平行四辺形になるための条件 まなびの学園

平行四辺形の証明問題 無料で使える中学学習プリント

File 平行四辺形の性質 2 Png Wikimedia Commons

平行四辺形の対角線の長さの求め方

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

平行四辺形の性質の利用２

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

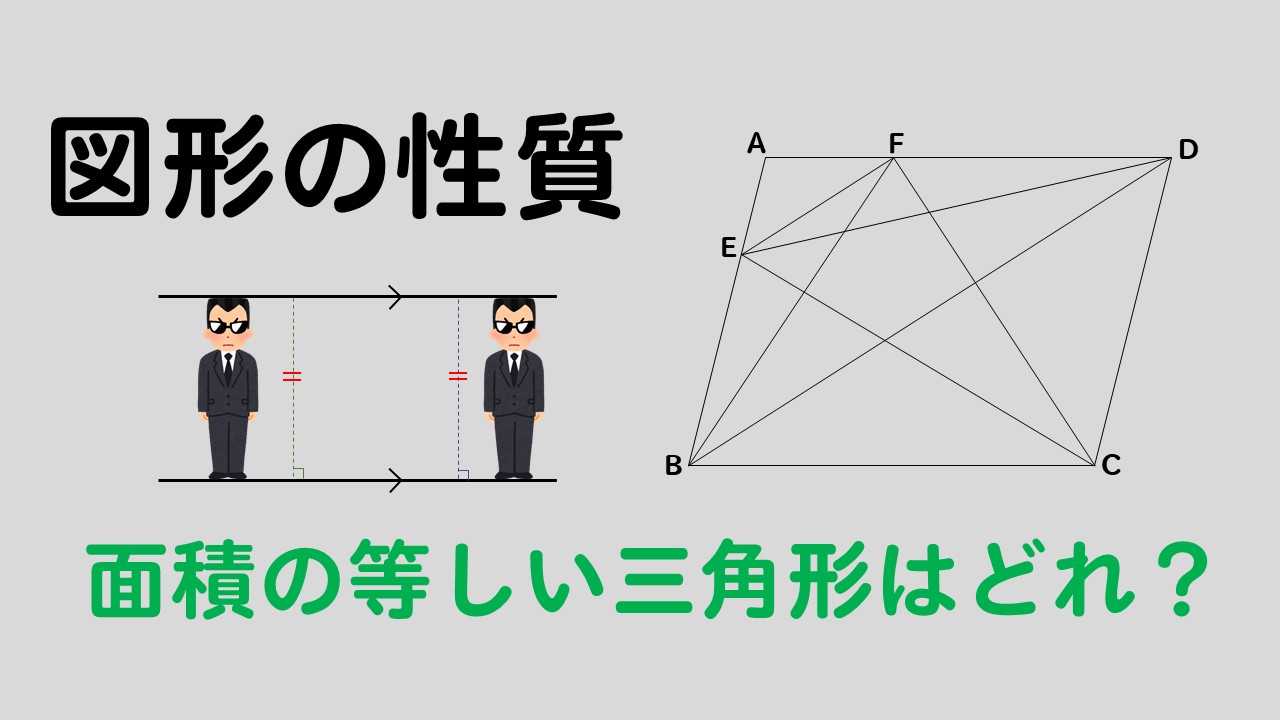
中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ

平行四辺形の性質

平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

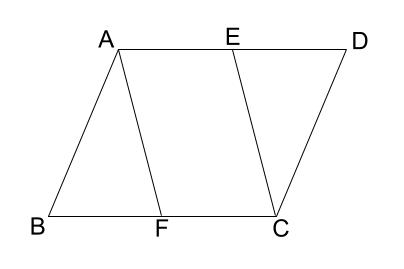
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su

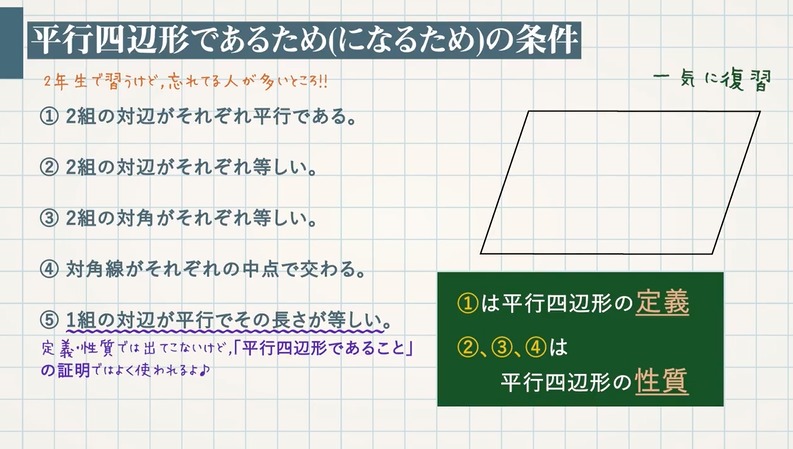
中点連結定理を使った平行四辺形であることの証明 教遊者

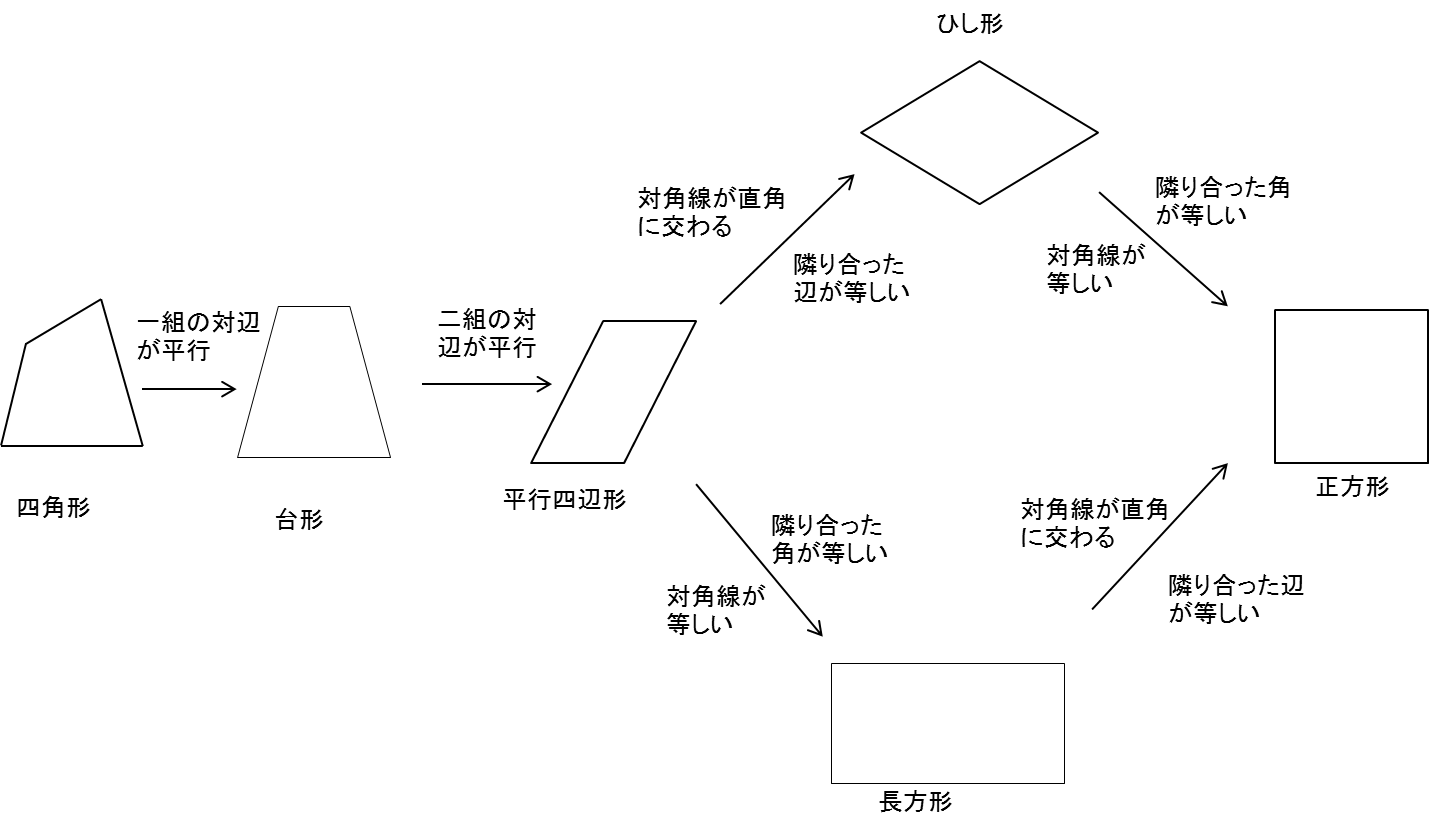
140字で高校受験 数学 四角形の性質まとめ 四角形 台形 平行四辺形 長方形 ひし形 正方形 高校受験 数学 T Co Tumufb1q86 Twitter